Excentricidad de una elipse

La excentricidad de una elipse es:

En donde a es el semieje mayor y c es la distancia del centro de la elipse a cualquiera los focos. La excentricidad es la razón de c y a. Entre más grande sea c, comparado con a, los focos están más lejos del centro. 

Ejemplos:

Elipse

Elipse es el conjunto de todos los puntos en un plano cuya distancia a dos puntos fijos en el plano tienen una suma constante. Los puntos fijos son los focos de la elipse.

 Elipse con centro (0,0)

Elipse con centro (h,k)

Ejemplos:

La Parabola

La Parabola

La parabola es el conjunto de puntos del plano que está a la misma distancia de un punto, su foco y de una recta fija, su directriz. Los elementos son:

               - El foco es el punto f

               - La directriz es la recta

               - El eje de la parabola es la recta que pasa por el foco y es perpendicular a la directriz.                        Tambien es un eje de simetria.

               - El vertice es el punto V en que el eje corta a la parabola

Para allar e foco se utiliza lo siguiente:

Ejemplo:

Para poder resolver una parablo con vertice (h,k), se utilizan las siguientes formulas:

Ejemplos:

Introducción a la Geometría Analítica

Secciones Cónicas: 

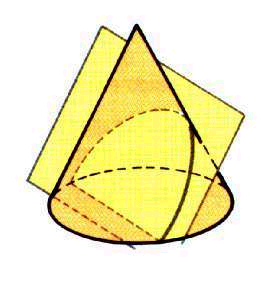
Una sección cónica es la intersección de un plano y un cono.
Dependiendo de la intersección, se obtiene una cónica determinada.

Si la intersección del plano es perpendicular al cono se obtiene: 

La circunferencia

Si el plano se inclina ligeramente la figura que se obtiene es:

  La elipse

Si un plano interseca dos ramas del cono, la curva resultante es: 

La hipérbola

nuando el plano es paralelo a una recta sobre el cono, la curva resultante es:

  La parábola

(En las próximas entradas se estará estableciendo información más detallada sobre esto.)

Teorema sobre la gráfica de y=a tan(bx+c)

Si y=a tan(bx+c) para números reales a y b diferentes de cero entonces:

(1) El período es π/|b| y el desplazamiento de fase es -c/b

(2) Asíntotas verticales sucesivas para la gráfica de un rama se pueden hallar al resolver la desigualdad -π/2<bx+c<π/2

Ejemplos de estos son:

Los ciclos de tan son -π/2,  π/2 y los de cot 0, π

Funciones cot, sec, cos

 Las siguientes expresan lo que serían las funciones cot,sec y csc y daría un ejemplo de una gráfica:

Teorema sobre amplitud y periodo

                                         Y= A sen Bx                 ó                          Y= A cos Bx

Para números reales A y B diferentes de 0 (cero), entonces la grafica tiene amplitud |A| y periodo 2π/|B|.

Algunos ejemplos de estos serian:

Teorema sobre desplazamiento de fase

                               Y= A sen (Bx + C)                         ó                         Y= A cos (Bx + C)

 Para números reales A y B diferentes de 0(cero), entonces :

                       - La amplitud es |A|, el periodo es 2π/|B| y el desplazamiento de fase es -C/B

                      - Un intervalo que contenga exactamente un circulo, se puede hallar al resolver la desigualdad:

                                                           0 ≤  Bx + C  ≤ 2π

Algunos ejemplos son: