Excentricidad de una elipse

La excentricidad de una elipse es:

En donde a es el semieje mayor y c es la distancia del centro de la elipse a cualquiera los focos. La excentricidad es la razón de c y a. Entre más grande sea c, comparado con a, los focos están más lejos del centro. 

Ejemplos:

Elipse

Elipse es el conjunto de todos los puntos en un plano cuya distancia a dos puntos fijos en el plano tienen una suma constante. Los puntos fijos son los focos de la elipse.

 Elipse con centro (0,0)

Elipse con centro (h,k)

Ejemplos:

La Parabola

La Parabola

La parabola es el conjunto de puntos del plano que está a la misma distancia de un punto, su foco y de una recta fija, su directriz. Los elementos son:

               - El foco es el punto f

               - La directriz es la recta

               - El eje de la parabola es la recta que pasa por el foco y es perpendicular a la directriz.                        Tambien es un eje de simetria.

               - El vertice es el punto V en que el eje corta a la parabola

Para allar e foco se utiliza lo siguiente:

Ejemplo:

Para poder resolver una parablo con vertice (h,k), se utilizan las siguientes formulas:

Ejemplos:

Introducción a la Geometría Analítica

Secciones Cónicas: 

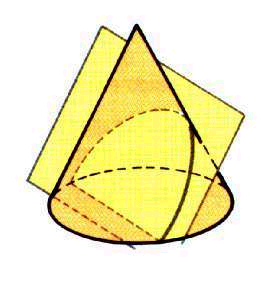
Una sección cónica es la intersección de un plano y un cono.
Dependiendo de la intersección, se obtiene una cónica determinada.

Si la intersección del plano es perpendicular al cono se obtiene: 

La circunferencia

Si el plano se inclina ligeramente la figura que se obtiene es:

  La elipse

Si un plano interseca dos ramas del cono, la curva resultante es: 

La hipérbola

nuando el plano es paralelo a una recta sobre el cono, la curva resultante es:

  La parábola

(En las próximas entradas se estará estableciendo información más detallada sobre esto.)

Teorema sobre la gráfica de y=a tan(bx+c)

Si y=a tan(bx+c) para números reales a y b diferentes de cero entonces:

(1) El período es π/|b| y el desplazamiento de fase es -c/b

(2) Asíntotas verticales sucesivas para la gráfica de un rama se pueden hallar al resolver la desigualdad -π/2<bx+c<π/2

Ejemplos de estos son:

Los ciclos de tan son -π/2,  π/2 y los de cot 0, π

Funciones cot, sec, cos

 Las siguientes expresan lo que serían las funciones cot,sec y csc y daría un ejemplo de una gráfica:

Teorema sobre amplitud y periodo

                                         Y= A sen Bx                 ó                          Y= A cos Bx

Para números reales A y B diferentes de 0 (cero), entonces la grafica tiene amplitud |A| y periodo 2π/|B|.

Algunos ejemplos de estos serian:

Teorema sobre desplazamiento de fase

                               Y= A sen (Bx + C)                         ó                         Y= A cos (Bx + C)

 Para números reales A y B diferentes de 0(cero), entonces :

                       - La amplitud es |A|, el periodo es 2π/|B| y el desplazamiento de fase es -C/B

                      - Un intervalo que contenga exactamente un circulo, se puede hallar al resolver la desigualdad:

                                                           0 ≤  Bx + C  ≤ 2π

Algunos ejemplos son:

Gráficas Trigonométricas

A continuación se mostraran las gráficas de las funciones trigonométricas básicas. 

 f(x) = senx

Esta gráfica corta por el punto (0,0)

El dominio de la funcíón es (-∞,∞)

El rango de la función es [-1,1]

Sus interceptos en el eje de x son: 0, π, 2π

Su intercepto en el eje de y es: 0

El periodo de la función es 2π

La amplitud de la gráfica es 1

f(x) = cosx

Esta gráfica corta por el punto (0,1)

El dominio de la función es  (-∞,∞)

El rango de la función es [-1,1]

Sus interceptos en el eje de x son:  π/2, 3 π/2

Su intercepto en el eje de y es: 1

El periodo de la función es  2 π

La amplitud de la gráfica es 1

f(x) = tanx

Esta gráfica corta por el punto (0,0)

El dominio de la funcíon son todos los números reales, menos π/2 y sus múltiplos.

El rango de la función es (-∞,∞)

Los interceptos en x son:  ...-2π, -π, 0, 2π, π...

El intercepto en el eje de y es: 0

Su periodo es π

La amplitud de la gráfica es infinita.

Fórmulas mitad de ángulo o semiángulo

Fórmulas para reducir las potencias

Las siguientes fórmulas presentadas nos permiten escribir cualquier expresión tronométricas que también contenga potencias de seno y coseno sólo en los términos de la primera potencia del seno. 

Ejemplosde fórmulas mitad de ángulo o semiángulo:

Formula de doble angulo

Las fórmulas de doble ángulo tienen la función de calcular el ángulo de cuando en el ángulo es doble.

Las fórmulas de doble ángulo son las siguientes:

 Algunos ejemplos de ejercicios donde utilizamos las fórmulas de doble ángulo serían: 

Formulas de Adición y Sustracción

Las formulas de  adición y sustracción están echas para buscar dos ángulos que sumados o restados den al ángulo dado.

Las formulas son las siguientes:

Ademas de las formulas de adición y de sustracción también están las formulas de cofusión. las formulas de cofusión se utilizan si la u, es un numero real o una medida en radianes de un angulo.

Ejemplos con cada una de las formulas de adición y sustracción:

Un dato muy importante para poder realizar este tipo de ejercicios es dejándose llevar o aprenderse la siguiente tabla:

Identidades Trigonométricas

 Las identidades trigonométricas son igualdades que contienen funciones trigonométricas y que son válidas para todos los valores de la variable que se considere.

Las identidades trigonométricas fundamentales son las siguientes:

Criterios para demostrar las identidades pitagóricas:

1. Elegir un miembro de la ecuación. Su objetivo es transformarlo en el otro miembro de la ecuación. 

2. Use el álgebra y las identidades ya conocidas para cambiar el lado con el que se empezó.

3. Escribir las funciones en términos de seno y coseno.  

Algunos ejemplos: